AMC数学竞赛如何做题效率最高？AMC竞赛备考PlanB高效解决

在机构的数学竞赛模考中，两位基础看似相同的小学霸，解决3道竞赛压轴题却形成了完全不同的答题样貌。

学生A：考试最后1秒才放下纸笔，时间紧迫，面对自己的答案表示未知，正确与否需要对标准答案才能知晓。

学生B：3道题均用多种解法轻松解决，最后还剩下10分钟检查答卷，用自己的其他解题方法进行论证后，表示“满分稳了”！

竞赛真题解析

如何选择最优的工具解决问题

在很多高级别竞赛题目中，一道题可能有很多种不同的解决方法，一般来说，在考场上，我们要选择一种效率最高的解决方法。之所以一道题会有不同的解题方法，主要是因为使用了不同的数学工具

同一道几何题，可以使用传统的几何方法（做辅助线，各种全等相似，各种定理推理等）、解三角形的方法、建坐标系、向量法、复数法等等；同一道代数题，也会有各种不同的方法。

但是不同的方法，思维的复杂度不一样，计算量也不一样，对于在考场上，时间有限的情况下，肯定要选择计算量小，而且思维复杂度低的这种。

先来看一道2018年AMC10数学竞赛B卷的一道题目：

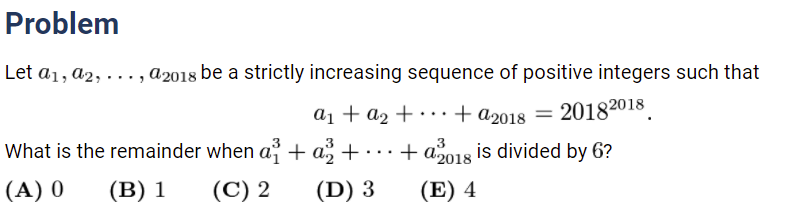
我们先看一种标准的解法：这种解法是使用了牛顿恒等式的一个推论（在韦达定理的扩展题目中也经常用到），同时使用简单的奇偶分析，可以快速做出来。

作为一道选择题，我们也可以采用特殊值法，这是我们第二种解法，比如：

当然类似的题目还有很多很多，再来看一道来自于AIME的考试：

明显的看出来，复数相乘的方法计算量要简单的多，下面这道清华的强基计划的题目，就更明显了：

构造复数相乘，比第二种方法就要简单很多。类似的题目还有很多，后续我们还会继续分享。

通过真题的分享不难看出：数学竞赛的本质还是选择最优的数学工具来解决你所面对的问题，在学会做选择之前，首先你要先熟练运用所有的数学工具。

这就是机构竞赛类数学课程体系的三部分：

基础段：学习然后熟练使用所有的数学工具；

强化段：学会做选择适合的数学工具来解决特定的问题；

冲刺段：以专题的形式再次强化解决问题的逻辑。

AMC竞赛备考Plan B 高效解决

从AMC的学习路径来看，AMC整个准备过程分为三个阶段：夯实知识点、串联知识点和冲刺刷题。

总体来看，整个备考过程需要学生：

先对单个的知识点的学习与深入挖掘，夯实学校不讲的但是竞赛会考的知识点；

随后将各个知识点的串联，锻炼数学思维和学习方法；

最后再通过刷题和模考，做好知识点的巩固和拉伸因此机构根据三个准备周期，整合基础课、强化课和冲刺课，一站式解决AMC备考。

对于学生来说：新知识点的掌握和很多考试中的解题技巧是必须攻克的难关，另外AMC题目解法很多，如果不讲时间控制总能做出来的，但考试是有时间限制的，从做题模式转换为考试模式也是难点。我们来看下各个阶段的准备需要花多少时间？

整体学习新知识点+操练简单题大概需要50小时左右，按照一周2小时学习的安排莱卡，基本需要25周左右。

对于学习融会贯通，熟练的使用并串联知识点，大概需要30小时，也就是15周时间。

最后对于考试前一个整套模拟，尽量是控制一个比较高的数量，以保证达到一个较好的手感和做题的状态，最好能每周进行模考，这个过程也大概需要30小时的时间。

而机构AMC10/12直通车班中涵盖的基础课程、强化课程和冲刺模考课程也是按照这样的时间分配，每周周末两小时，高效备战AMC冲奖晋级。