AMC10难不难？AMC10题目难度分析答题技巧分享

距离 AMC10 开考不足50天时间，你不可不知的备考技巧都在本文为你汇总完毕，记得收藏好！

选择题答题技巧

❶ 设数法

➤ 方程个数少于变量的时候，可以假设其中某些变量为特定值（不适用于整数方程）；

➤ 递推数列的前几项是比较大或者复杂的数时，可以自己假设一些简单值或者直接假设变量进行递推，可能会有周期性或者明显的规律；

➤ 当几何图形不唯一时（即拥有一定自由度时），可以假设某些特殊条件（例如某个特殊角度或者某条边长），然后再进行计算。

❷ 度量法

对于部分几何题，如果题目条件能够唯一确定图形时，可以作出标准图；当题目条件不能唯一确定图形时，可以画出某种特殊情况下的图形。而后可以通过度量边长或者角度直接得到答案（但是近年来出题人会有意规避这种可能，所以能用到的机会不大）。

❸ 找规律

递推数列、递推函数、新定义的数论函数、组合递推问题、二人游戏问题，都可以先从最简单的初始情况开始研究，争取发现规律。

❹ 排除法

根据奇偶性、特定的因数、取值范围等，可以排除掉某些选项。（但是部分题目的答案是经过改造的，这样排除法就不适用，例如最后答案是n/m，求n+m的值）。

Tips & Notes

❶ 在考试前就确定自己的答题策略：

➤ 做不出的题目是要猜答案还是做不出一律空着？

➤ 如果猜答案的话，那么排除多少个选项后再猜？

➤ 目标是做到第几题，做出多少题？

➤ 做完前10题预计要多少时间，11-15题多少时间，16-20题多少时间？

➤ 最后留多少时间来检查？

❷ AMC10部分需要记住的公式其实不多：

➤ 代数：二次方程求根，多项式韦达定理，等差等比的通项和求和，二项式定理；

➤ 坐标系：点到直线距离，鞋带定理；

➤ 几何：勾股定理，角平分线定理，特殊直角三角形的比例关系，常见图形的面积和体积公式；

➤ 数论：因数个数/和/乘积，阶乘的质因数分解，因式分解公式

❸ 在应用题、几何题、数列题、函数题中，如果题目中的变量都是整数时，很有可能是数论题目，需要用到数论相关知识，例如分析因数和倍数关系或者列出整数方程再求解。

❹ 概率类题目，要搞清楚是否为几何型概率，是否是无穷状态类问题，是否是equally likely outcome型概率，然后再选择对应的方法。

❺ 两人游戏类问题，简单情况可以直接枚举进行讨论；复杂情况可以先用matching（配对）和mirroring（镜像）的特殊方法进行尝试，若不行再从简单的初始条件出发，寻找winning position和losing position，并找出一般规律。

❻ 善于利用对称性化简问题：组合计数题目可以根据对称性减少需要计算的情况（例如给正方体染成2黑4白和2白4黑的情况是一样的）；具有对称性的方程组可以尝试相加或者相减，再进行因式分解；光线传播类问题需要对图形作对称让光线沿直线传播。

❼ 熟悉函数图像的画法：基本函数（线性、二次、指数、多项式、有理函数）、特殊函数（绝对值、取整函数）、复合函数图像，以及图像的平移、伸缩和对称变换。考前可以自己用画图软件在研究一下各类图像的画法。

❽ 有些试卷后10题的难度差异不明显（例如2021AMC10A卷和2021AMC12B卷），因此建议大家考试时至少看一下后5题，如果有自己熟悉的题型可以尝试做一下。

答题策略

1-10题正常按照顺序做，当感觉到题目变得复杂时（大约是从第10题附近开始），可以考虑以下策略：

➤ 均衡型：如果自己不同模块的水平比较均衡，可以按照题目顺序进行答题，每道题目控制好时间，一道题目上卡了太久就及时跳过。

➤ 模块回避型：如果自己在某一模块上明显薄弱（例如组合），那么就先全部跳过此类题目，完成其他题目后若还有时间再回过头来做这类题目。

➤ 模块优先型：若自己不同模块的水平差别十分明显，那么建议可以根据自己不同模块的水平，从高到低依次解答剩余题目。例如几何最强则先做几何，组合最弱则最后做组合。

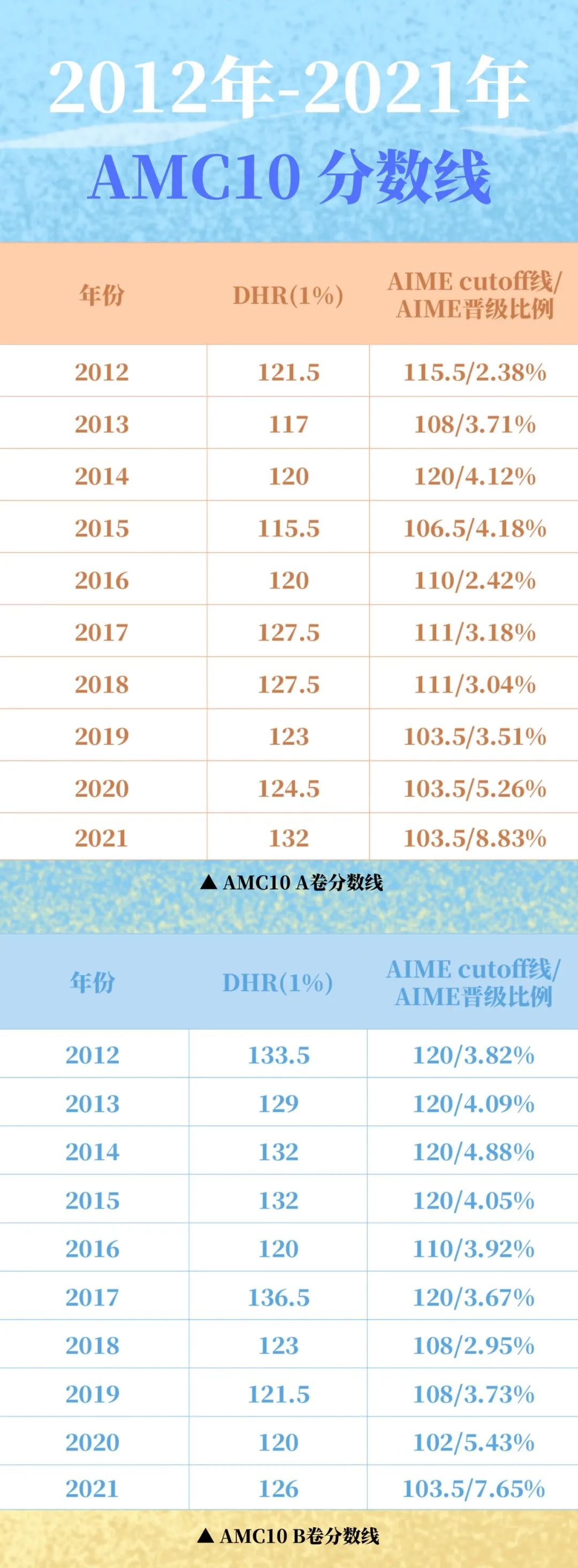
历年分数线