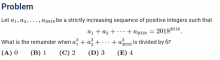AMC12是什么？AMC12竞赛难度如何？

不知道最近大家有没有发现身边的小伙伴们纷纷开始收集一沓神秘的数学卷子，同学们不要慌，他(她)做的是AMC12的考试真题。

什么是AMC12？

AMC12是由美国数学学会(MAA)组织的美国数学竞赛最高组别比赛，参赛对象为12年级及以下高中生，对应国内高三、高二年级学生(高一及以下的学生也可报名参加)，每年举办两次考试(两次考试相隔一周)，考生可择一参加，考生能够拿到的奖项分别为AIME Qualification(前5%)以及Distinguished Honor Roll(前1%)。

越来越多的申请生投入到这门超具“含金量”的硬指标考试中，AMC12除了是对“智商”的绝对挑战以外，也因为较高的门槛和较低的入围率(5%)成为表现自己理工科能力的最好证明！ 

AMC12有多难？

说这么多，那么AMC12考试到的难度到底如何呢？同学对这个问题的看法大体分为两类：一类理所当然抱着轻视态度，认为美国的数学比赛会像sat数学一样简单；另外一类同学往往在做过一两道难题以后就立马退缩了。 其实对AMC考试难度过高或过低的预期都是有所偏差的，你只需要具备：

相对扎实的数学基础知识以及较强的计算能力；

比传统标化考试更灵活的数学思维模式

就可以达到备考AMC12的基本要求；我们今天就来尝试着通过2道真题为大家展现一下AMC考题的难度大概是怎么样的。

题目①：2016B真题第14题

这道题目在AMC考试里难度适中，只要用到两个基础的知识点（Infinite Geometric Series的求和公式 + Quadraticfunction的max/min）就可以完美地解决这道问题。

Step1：我们可以将这个Geometric Series的公比设为r，那么根据Infinite Geometric Series的求和公式a/(1-r)来看它的sum应为 (1/r)/(1-r), 再将其转化成1/(-r^2+r)的二次函数倒数形式；

Step2：既然是让求它的最小值，其实也就是求得(-r^2+r)的最大值1/4，并得到最终答案为4；类似这类题目，对于想要打入AIME的同学，这是一定要抓住的分数。

这也是我们一开始说的，对于准备要开始备考AMC12的同学来说，具备相对扎实的数学基础知识是十分重要的，这能够确保我们有学习竞赛的基础，也有助于我们拿到必须拿到的分数。

题目②：2016B真题第20题

我们再来看一道比较难的题目，这道题题目的意思是：一个体育联盟内部总共有21只球队，每只队伍和另外20个对手分别比赛一次，且“恰巧”每只队伍都是赢10场、输10场，问：能选出多少个满足“A克B、B克C、C克A”的组合？ 这道题乍一看“难爆”了，因为正面思考这个问题的最大难处在于分支太多，很难直接用排列组合计数原理的思想去做。但其实这道题我们反面思考问题会简单的多： 

Step1：利用互补的思想：三个队形成的组合只有“A克B、B克C、C克A”以及“A即克B又克C，BC之间随意”两种情况；

Step2：用计数原理迅速算出第二种情况为(21)*(10C2)=21*45=945种情况(分别从21支队伍的10支战胜队中选出两支，形成一个三队组合)；

Step3：只需在用21C3(所有可能组合) - 945=385即可得到答案。所以这道题目考察的更多的是我们灵活的思维模式，对于AMC12考试的题目而言，有时候传统的正向思维会使得题目看起来十分困难，但是换个角度解题兴许就有“柳暗花明又一村”的感觉，而培养学生们的发散解题思维也是TD「AMC备考计划」的授课目标之一。

AMC12不容易，但是或许你也行

通过刚刚的两道题目，已向大家展示了大致展现了AMC12考试难度，整体来说它需求考生应该拥有以下两种能力：

1. 相对扎实的数学基础知识以及较强的计算能力

我们发现AMC考试的内容主要集中在初高中的数论、计数原理、代数、函数、平面立体解析几何这几大块知识点内，可以说学过precalculus或者等价课程的同学都完全有能力涉足AMC并用相关知识解题，但因为AMC是一门对答题速度有极大苛求的考试，往往需要同学们拥有很强的计算速度与计算准确度。

2. 比传统标化考试更灵活的数学思维模式

改变以往的数学思维模式，“多”学一些更高阶的知识，提高解决问题的技巧，往往会带来一些意想不到的效果。比如一道用常规方法很难很耗时的题目，如果大家多学一些知识（比如Calculus、Linear Algebra等），“一道难题”在大家手里就变成了“一键解题”，这种剑走偏锋的思路是没有经过训练的同学的软肋，但学到了性价比往往很高。

总之，大家不必妖魔化AMC题目的难度也不能低估，在数学基础和解题技巧两个方面齐头并进才是最终拿到入场券的正确思路。