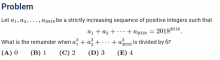AMC数学竞赛代数题例题解答
AMC不同于其他的数学比赛,它的体系环环相扣,颇有打怪升级的感觉。
对于中国学生来说,AMC 8/10/12,包括之后的AIME都是可以参加的,但再往上的USAMO则是为了选拔美国奥数国家队队员设立的,相当于我们国内的“国家集训队”,只有美国公民或美国/加拿大的合法居民可以参加。
而对于名校申请,特别是MIT、斯坦福、普林斯顿,光从AMC晋级AIME还不够,如果AIME成绩要达到晋级USAMO的成绩,则更有优势,因为每年晋级USAMO的学生人数不超过300人,是当年全美乃至全北美洲数学最强的学生,极其受到藤校的青睐。
随着参赛人数逐年增加,想在AMC中胜出越来越难,我们也为大家准备了AMC四大题型及解题秘笈。
AMC四大题型及解题秘笈
AMC数学竞赛代数题例题解答
AMC数学竞赛几何题例题解答
AMC数学竞赛数论题例题解答
AMC数学竞赛排列组合及概率题例题解答
题型一:代数题
“代数”(Algebra)起源于古巴比伦时代,词源是阿拉伯语单词“al-jabr”,意义为“重聚”。代数的方法,让古巴比伦人发展出了较之前更进步的算术系统,而同一时期的埃及人、印度、希腊和中国数学家则一般是以几何方法来解答同样的问题。
初等代数在国家大纲里是从五年级开始学习,相对于之前的学习内容,一个显著的特征是,引入了用字母符号来“代替“数字,并且对符号进行形式化的运算。在此基础上,再发展到方程和函数等概念的建立。
虽然代数是要以符号来代替数字,但是初涉代数的学生往往不好理解这种抽象性,总是试图在符号上面“代入“具体的数字去运算。虽然这不失为一种让学生通过试探,逐步从具体思维发展到抽象思维的方法,但是只有当学生不再试图“代入”具体数,代数不“代数”的时候,才是真正开始掌握代数的标志。
2015年AMC8的第24题,倒数第二题,是难度比较大的。

解题思路:在这个题里面,N和M虽然实际上是确定的数,但是以未知数的形式出现的。初学的同学会对N和M的数值进行各种尝试和代入,从而缩小范围,这样是很有可能得出正确答案的。然而,正规的代数方法是先根据条件列出一个方程,因为有两个未知数,但是只有一个方程,所以是不定方程。不定方程在限定条件是可能有唯一解或者有限个数的解的,这里的限定条件就是N和M都是整数,N>2M和M>4,这些限定条件排除了不可能的解,剩下的就是我们要的解。