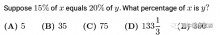AIME考试都考哪些知识点?2023年该如何高效备考AIME?

AIME考试都考哪些知识点?2023年该如何高效备考AIME?AIME 考察的知识点，会覆盖代数，几何、数论、组合这四个范围的知识点。知识点覆盖情况，重要性：几何、代数>数论>组合。

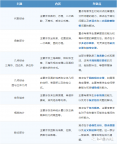
除组合之外，其他考的题量还是比较稳定的。几何、代数占的比较多，但代数涉及的知识点更多。数论和代数相结合也是经常考察到的。组合很多时候和集合相关，不是很难。各学习板块知识点覆盖范围可参考下图

 

 

相比AMC，AIME在深度和广度上都有扩展，尤其是深度上。AIME备考建议最好去关注经常考的/考过的知识点，不用学比较难的定理。并且最好有专业老师引导和对常考知识点有个全面把控，并进行针对性训练，这会比一味地灌溉比较难的定理意义更有用。

AIME考点：代数 (Algebra)

复数：复数的几何意义、单位根、欧拉定理

多项式:代数基本定理、因子和余数定理、韦达定理推厂

解方程与不等式：多元高次方程，柯西不等式

其他:函数图像、三角恒等变换、数列与数学归纳法、集合划分、指对数等

10-15的复数题用代数解非常麻烦，这是要考察它的几何意义，还可能考到单位根。复数、多项式一般都是结合起来考。

三角恒等变换：尤其是国际学校同学，三角函数知识相对薄弱，这里的三角恒等变换不仅是基本的三角公式，也不是解三角形的问题或者三角函数的图像性质，它指的是一些特殊角度/一些恒等式。还是属于代数的范围，但是技巧性要求比价高。

集合的划分：函数的定义是要建立在集合的映射上，所以集合是近几年AIME考察的重点。

AIME考点：几何

平面几何(Geometry-Plane)

三角形定理：海伦公式、三角形五心、梅涅劳斯和塞瓦定理

圆相关：相切问题，托勒密定理、圆幂定理、根轴

四边形相关:四点共圆

思想方法：解析法、三角法、几何变换等

解析几何：圆锥曲线

立体几何：几何体的相切

考试建议：考试时可以先做几何、代数这些相对简单的题目。

AIME考点：数论(Number Theory)

整数的性质:整除、数位、质因数分解、最小公倍数和最大公约数、同余等

数论定理：裴蜀定理、费马小定理、威尔逊定理、中国剩余定理阶等

不定方程：因式分解、取模、不等式法、佩尔方程

AIME考点：组合(Combination)

排列组合：组合恒等式、容斥原理、组合计数

概率:古典概型、几何概型、递推、条件概率

思想方法：对应、算两次、最值原理

说明：蓝色字体为AIME额外会考的知识点，须重点学习!

其他列举的考点在AMC10/12的竞赛考试中已考过。知识点若已全部掌握，可放少部分的时间及精力在其上面。多做精编习题，巩固并加强知识点的灵活运用。