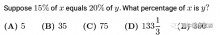AMC8数学竞赛获奖率高吗?有什么优势?
美国数学竞赛AMC8
低年级绝不能错过的国际数学竞赛
入门指南 赛事详解 备考攻略

为什么如此看重AMC8?
国际认可度高
AMC8数学竞赛历史悠久并且国际中有较高的认可度。从1985年开始了第一场比赛,AMC8持续至今,带动了很多数学少年的学习热情,也给全世界的数学少年一个交流和竞技的舞台。是全美排名前五十名名校、全美几乎所有中学优先推荐的主要活动之一。
助力名校申请
AMC可以说是美国数学的人才库,为各大名校申请者的数学学习成绩提供了一定的参考和评估。AMC8的成绩对于申请美国初中与美国高中起到了至关重要的作用,是学术能力证明。
数学竞赛的开端。
数学竞赛的开端
AMC8算是数学竞赛的开端,这个阶段学得全面且踏实,对于AMC10/12的晋级肯定有直接的影响。毕竟数学竞赛体系一脉相承,卡耐基梅隆和布朗等名校的申请界面都需要学生填写AMC10、AMC12和AIME的成绩,说明名校已经开始认可AMC作为升学条件。参加AMC8把功底打好,后续不愁。
题目设计新颖
AMC8数学竞赛难度逐题递增,题目设计新颖有趣,对没有竞赛基础的同学仍然相对友好。AMC8作为AMC系列的第一个考试,25道题中,前10道题难度不大,并且总体上题目的设计比较有趣,所以很多学生都愿意进行尝试。
参加AMC8能给学生什么优势?
1.由于AMC考试成绩国际通行,因此其成绩成为学生增加国际竞赛经验、提升学生国际化学习和竞赛背景、提高入学竞争力的重要途径。
2.虽然AMC是一个竞赛考试,但是题目由浅到深,且具有很大的趣味性和研究性,不同基础的同学都能从中感受到数学的乐趣和挑战。
3.对数学很感兴趣的同学,参加AMC不仅能在数学学习技巧上得到很大的提升,也能认识一群志同道合的朋友,为以后的数学研究奠定了基础。
4.参加AMC会得到一份官方出具的“参赛证书”。中国学生在数学上的得奖率超过了世界一倍。能够在AMC竞赛中获得相应的奖项,成为了未来申请美国和加拿大名校的重要砝码。
AMC8的获奖率高吗?
国际认可度高
AMC8的考点与7、8年级数学大纲相对应,包括(但不局限于)整数、分数、小数、百分数、比例、数论、日常的几何、面积、体积、概率及统计、逻辑推理等。
题目难度分析
AMC8一共25道单选题,从第1题到第25题难度是循序渐进的:
第1题-第10题:不会特别难,都是基础题目。 第15题-第20题:相应会有一些难度,而是同样水平的难度,只是考的题点不一样。 第16-第20题:这五道题对学生来说非常重要,尤其是冲击5%的学生,考试技巧很重要,因为答对一道加1分,答错不扣分,所以需要注意守住自己的策略分。历年平均分
| 年份 | HR(前5%) | DHR(前1%) |
| 2020 | 18 | 21 |
| 2019 | 19 | 23 |
| 2018 | 15 | 19 |
| 2017 | 17 | 20 |
| 2016 | 18 | 22 |
| 2015 | 16 | 21 |
| 2014 | 19 | 22 |
| 2013 | 17 | 22 |
| 2012 | 17 | 22 |
结合分数线情况不难看出,AMC8 的难度整体上呈现稳定升高的趋势,最高奖项基本要达到20分以上才有希望,这对学生的数学技能和答题技巧都有很高要求。建议及早准备,提前夯实基础,做好充分准备。
奖项设置
| _ | 满分奖PerfectScore:获得满分25分的同学 |
| _ | 全球卓越奖Distinction Honor Roll:全球排名前1%,一般为22分左右(满分25) |
| _ | 全球优秀奖Honor Roll:全球排名前5%一般为17分左右 |
| _ | 成就证书Achievement Roll:6年级以下学生,且分数≥15 |
AMC8竞赛规则
考试对象:主要面向8年级(初二)以下的初中和小学高年级学生 竞赛语言:
中英文双语 考试时间:
每年的1月份 报名日期:
每年9月-12月 报名方式:
联系竞赛小助手 题目类型:
25道单项选择题 (时间40分钟) 评分规则:
答对一题得一分,答错不扣分,满分25分 考试地点:
全国各考点学校;
在线考试,需配备带摄像头的电脑及手机移动设备 成绩公布:
考试后约4周(不超过4周)
备考攻略
知识点梳理
很多临时做一些真题然后就开始参加考试,获得高分的概率特别低。所以在考试前要把考试的知识点梳理一遍,对考试的内容有一个整体的了解,并且找出一些重点难点的部分进行深入复习,考试的时候才能胸有成竹。
刷真题
刷真题是备考最重要的一个阶段,经过前面知识的积累,要进入实战阶段,磨炼技巧和速度。最好能刷5-10年的真题,每年有AB两卷,也就是10-20套卷子。虽然每年的题型有所变化,但是知识点是一样的。
考试策略
从真题错题中找出自己觉得比较难的知识点,并且再次加深理解。对错题的知识点进行拓展。有意识地锻炼自己的做题速度,并且针对题目的难易程度进行取舍。答题时注意灵活运用,当正常解题思路遇到困难时,可以尝试排除法、特殊值带入等方法高效地帮助我们在选择题目排除错误选项,从而选择出正确的选项。