AMC美国数学竞赛难度大吗?最后五题详细解析!
AMC美国数学竞赛难度大吗?最后五题详细解析!随着标准化考试越来越普遍,仅仅靠优异的高中均分、雅思托福等成绩越来越难在一众优秀的申请人中脱颖而出,数学竞赛成绩就成了高手如云的名校申请中的制胜法宝。
欧几里德数学竞赛相信大家并不陌生。作为加拿大本科申请的重要衡量标准之一,在竞赛届极其出名。
但是其参赛年龄大部分为十年级以上。不少八年级的同学总是来问,有什么竞赛适合同样对数学学科充满热情的我们呢?什么竞赛锻炼我们解决问题的能力,也同样为未来的大学申请加分?
今日学长就来帮大家扫盲这些适合八年级左右的中学生们参加的高阶竞赛。第一篇让我们来聊一聊美国数学竞赛(American Mathematics Competitions)。
AMC是目前世界上规模最大且最具公信力和高校认可度的竞赛之一。2020年美国数学竞赛AMC-8的成绩刚刚出炉。受疫情的影响,据美国数学协会(Mathematical Association of America)官网数据显示,参赛学生人数只有5万5千人,相比这几年来的平均参赛人数下降了约40%。
但是本届的题目难度基本和往年相当。今年Distinguished Honor Roll(top 1%)的分数线是答对21题,Honor Roll(top 5%)的分数线是答对18题。
小编为大家介绍一下最后五题精准解析
1Problem 21

这题我们很容易想到,从水平方向上从P到Q一共是7步,每步不是往左一格就是往右一格,7步加一起最后是往右了一格,所以应该是4个右,3个左的排列组合问题,一共是C(7,3)=35种。
但是这样其实就错了。因为我们忽略了一个问题,就是这个game board是有大小限制的。比如,一开始不能连续往右走3步,因为那样就超出了棋盘的范围,因此35种情况是要扣除一下超出棋盘的情况的。不幸的是这个35还是5个选项中最大的一个答案,所以对排除错误答案还一点帮助没有。
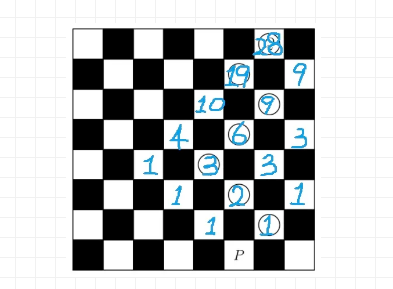
因此从这题的解法上看,倒还不如一开始就用枚举法一层一层往上试着推一下来的方便。我们可以看出,第1步可以往左或者往右,所以各有1种可能。到第2步,又可以容易的推出可以到达3个格子,一共4(1+2+1)种可能的走法。到第3步,又可以得出1+3+3=7种可能。照这个规律依次类推,很容易我们就可以推到第7步到Q点,一共是19+9=28种可能,选A。
2Problem 22
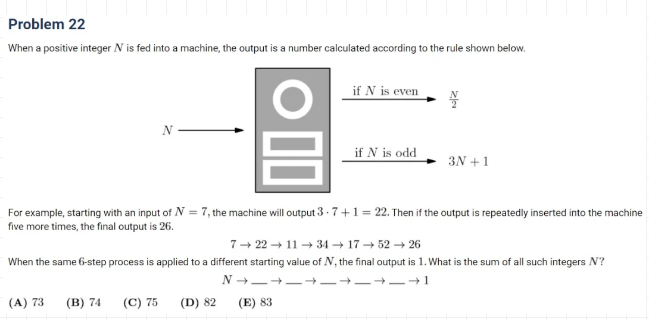
这题比较简单,这里的machine其实就是函数(function)的概念,我们用倒推法可以方便快速的解决。因为最后输出的结果是1,而N是大于0的整数,所以3N+1不可能得到1,只能从N/2这条路得到,所以倒数第二个输出结果只能是2。
同理,如果结果是2,则不可能是3N+1(因为是奇数),所以倒数第三个输出的结果只能是N/2这条路得到,所以倒数第三个输出结果只能是4。而4可以是8/2=4或者3*1+1=4得到,所以倒数第四个输出结果就有2种可能了,一个是8,另一个是1。就这样我们依次类推到第一个输入数字的所有可能,如下图,就可以得到最初的N有4种可能,64,10,8,1。所以答案是83(E)。
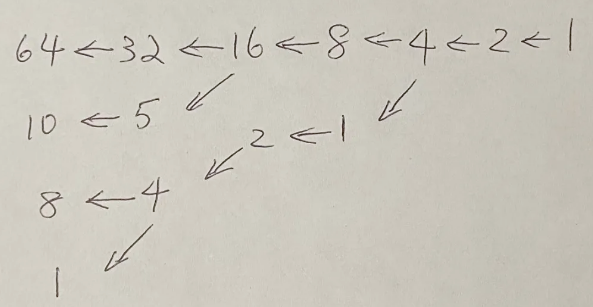
3Problem 23

这题属于比较难和繁琐的排列组合类题目。5个不同的奖分给3个不同的人,所以一共是35 =243种可能(每发1个奖可以有3选择)。
但是要扣除2种情况:
有1个人完全没得奖而其余2个人得奖的情况
只有1个人得奖的情况
对于第一种情况,假设是第一个人没有得奖,另2个人得奖。那么情况就相当于2个人分5个奖,25 种。但是这里又要扣除2个人中只有1个人得奖的2种情况,因为这就等于是1个人获了所有的奖,属于我们后面要考虑的第二种。
所以第一个人没得奖,后面俩都得奖的情况有25 - 2=30种。同理如果是第2、3个人没有得奖也是一样。所以第一种情况有30*3=90种。
对于第二种情况,如果只有一个人得奖,则显然只有3种情况。因此,这题的答案是243-90-3=150种(B)
4Problem 24
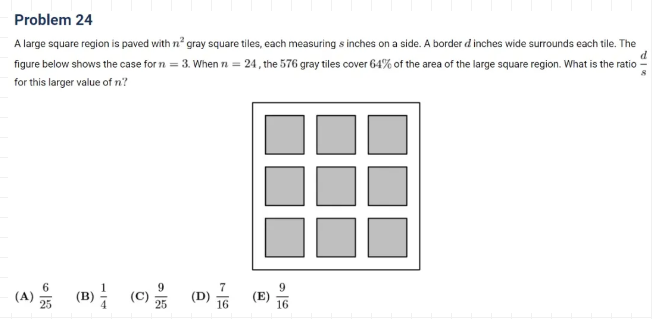
这题属于简单的面积计算,类似题在历届考试题中有出过。这类题的技巧是尽量不要去死算边界面积,而是要用简单的正方形面积去计算。同时在这道题里要注意的是平方数要先保留平方,小数要转化为分数表达等小技巧,这样帮助迅速计算出答案。
n=24时所有gray squares的面积和是242 *S2 , 而整个大正方形的边长是24S+25d,所以面积是(24S+25d)2 。题目说
d/s=242 *S2 / (24S+25d)2= 64% ,所以我们只需要做如下化简就可以得到答案了。
先去掉上面等式两边的平方,于是得到 24S/(24S+25d)=0.8 。 然后改用分数4/5来表达小数0.8,同时等式两边分别取倒数来简化,就可以得到等式1+25/24*d/s=5/4。最后再变换一下算得d/s=1/4*24/25=6/25, 选A。
5Problem 25
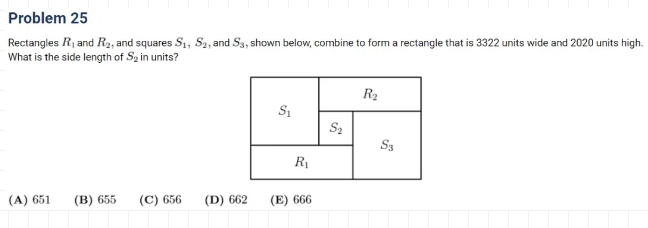
这题其实相当简单,简直是送分题,关键是很多同学可能没有时间做到这题了。我们假设正方形S1,S2,S3的边长分别是X1,X2,X3。那么可以很容易的看出,X1+X2+X3=3322, X1-X2+X3=2020。把这两个等式相减马上得到2*X2=1302,所以X2=651,选A。
是不是送分题?所以竞赛的时候临场的时间控制很重要,至少每题要有一定的时间扫一眼,否则像这样简单的最后一题没时间做就亏了。